今後の社会イノベーション事業では,社会システムの最適化の際に組合せ最適化問題を解く必要があり,それを効率よく実現する新しい原理のコンピューティング技術として,イジングモデルを用いたCMOSイジング計算機を提案している。
これまでに第一世代のプロトタイプとして2万スピンを含んだイジングチップを65 nmプロセスで試作しており,今回,FPGAを用いた第二世代プロトタイプを構築した。CMOSイジング計算機の実用化に向けて,ハードウェアに加え,ソフトウェア技術の開発も推進している。また,複雑な社会問題を単純で規則的なハードウェア構成に埋め込むためのグラフ埋め込み技術を開発し,従来技術よりも高速に問題をイジング計算機に載せられることを確認した。





社会の持続的な発展とさらなる快適性を追求していくうえで必須となる社会イノベーションを実現するには,豊かな社会を実現するインフラ技術と高度なITの組合せが必要となる。これまでのITは,スーパーコンピュータに代表されるように多くの数値計算を行うことに主眼が置かれてきた。しかし,社会イノベーションの実現には,社会システムの最適化が必須となる。例えば,交通システムや物流システム,電力グリッドなどでは,車の流れや配送経路,電力の流通量などを最適化する必要がある。こういった最適化には,組合せ最適化問題と呼ばれる問題を解く必要があるが,従来の計算機では,組合せ最適化問題を効率的に解くことは困難である。
そこで,われわれは,社会イノベーションを実現するためのコンピューティング技術として,組合せ最適化問題を効率的に解く新しい概念のコンピューティング技術を開発した。本稿では,この新概念コンピューティングに関して解説する。
組合せ最適化問題とは,与えられた条件の中で評価指標を最大(または最小)とするパラメータの組合せ(解)を探索する問題である。決定するパラメータの数が多くなると,その問題の解の候補が爆発的に多くなるという特徴がある。
従来の計算機で組合せ最適化問題を解く場合には,問題をプログラム(手順)に分解し,そのプログラムを順次実行していた。しかし,組合せ最適化問題では,パラメータ数が多くなると解の候補が爆発的に多くなり,計算時間も飛躍的に増加する。
本章では,これを解決するための新しい概念のイジング計算機と,われわれが提案するCMOS(Complementary Metal Oxide Semiconductor)半導体へ実装したCMOSイジング計算機について説明する。
組合せ最適化問題を効率よく解く手法として,磁性体のスピンの振る舞いを表す統計上のモデルであるイジングモデルを用いた手法が提案されている。
イジングモデルを図1に示す。イジングモデルは,磁性体の性質を表す上下の向きを持つスピンの状態σiと2つのスピン間で及ぼす相互作用の力を表す相互作用係数Jij,および外部から与えられた磁場の力を表す外部磁場係数hiで表される。そのイジングモデルが持つエネルギーHは同図中の式で表される。
イジングモデルでは,そのエネルギーHが最小となるようにスピンの状態が更新される。組合せ最適化問題の評価指標を,このイジングモデルのエネルギーに対応するように問題を写像して,イジングモデルを収束させることにより,エネルギーを最小とするスピンの状態の組合せが得られる。それはすなわち,元の最適化問題の評価指標を最小化するパラメータの組合せを求められることを意味している。
図1|イジングモデル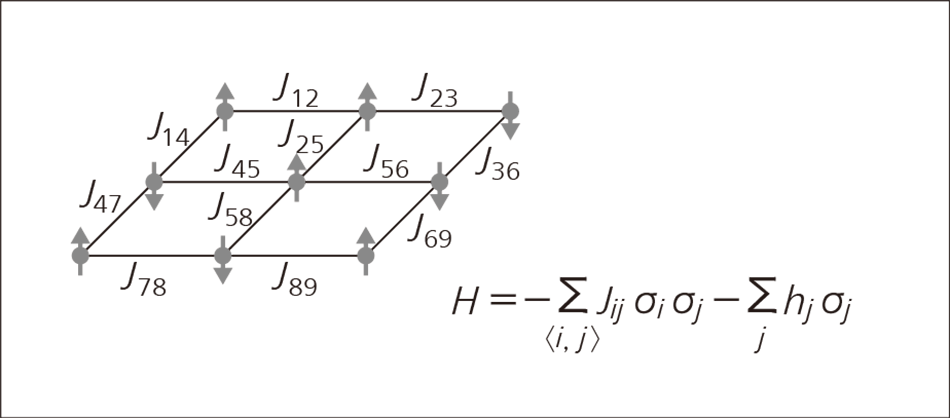 共磁性体の性質を表す統計力学上のモデルである。2つの配位状態をとる格子点(スピン)から構成され,隣接する格子点の相互作用を考慮したエネルギーHが最低の場合に安定状態となる。
共磁性体の性質を表す統計力学上のモデルである。2つの配位状態をとる格子点(スピン)から構成され,隣接する格子点の相互作用を考慮したエネルギーHが最低の場合に安定状態となる。
図2|イジングモデルのエネルギーランドスケープとCMOSアニーリング
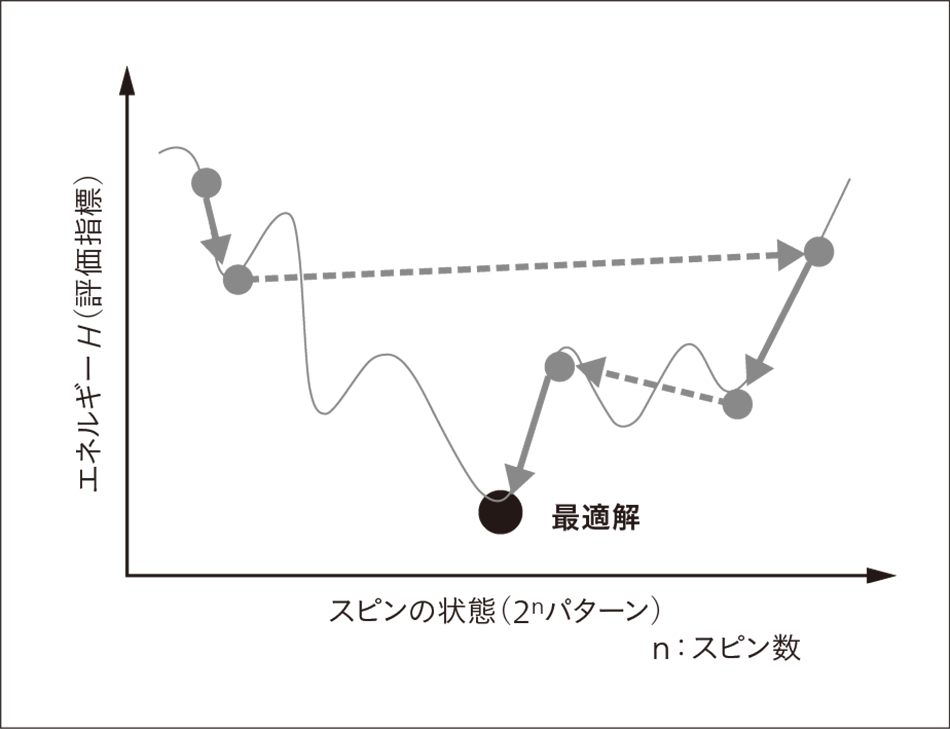 CMOS(Complementary Metal Oxide Semiconductor)イジング計算機では,スピン間の相互作用によりエネルギーはランドスケープにしたがって減少する(実線矢印)が,局所解に固定される可能性がある。乱数を入力してわざとスピン値を反転させることで(点線矢印),局所解への固定を避ける。これにより,エネルギーの低い解が求まる。
CMOS(Complementary Metal Oxide Semiconductor)イジング計算機では,スピン間の相互作用によりエネルギーはランドスケープにしたがって減少する(実線矢印)が,局所解に固定される可能性がある。乱数を入力してわざとスピン値を反転させることで(点線矢印),局所解への固定を避ける。これにより,エネルギーの低い解が求まる。
イジングモデルを,半導体のCMOS回路を用いて模擬することを提案した1)。CMOS回路を用いることで,製造が容易で拡張性が高く使いやすいという特徴がある。
イジングモデルを模擬した回路では,スピン間の相互作用動作によって,イジングモデルが持つエネルギーはエネルギーランドスケープにしたがって低下する(図2参照)。しかし,同図に示すようにエネルギーランドスケープには山と谷があり,相互作用の動作のみでは,局所解と呼ばれる最小のエネルギーではない部分にとらわれてしまう可能性がある。この局所解から脱出するために,ランダムにスピンの状態を破壊する効果を持たせる。これにより,同図の点線のように関係ない状態にランダムに遷移させる。この2つの動作を合わせてCMOSアニーリングと呼ぶ。これにより,できるだけエネルギーが低い状態を見つけることができる。
実際には,乱数を用いているため,必ずしも最適な解が求まるとは限らない。しかし,この計算機を社会システムの最適化に使う場合には,最適値でなくても許容できると考えられる。例えば,物流の経路を求める際に,経路全体の値が多少大きくなっても,システム最適化の観点からみれば許容可能であると考えられる。
提案したCMOSイジング計算機の動作を実証するためにプロトタイプを試作した2)。第一世代のプロトタイプは65 nmプロセスを用いたイジングチップで構成され,CMOSイジング計算機のスケーラビリティを実証した。第二世代のプロトタイプは再構成可能なLSI(Large-scale Integration)であるFPGA(Field Programmable Gate Array)を用いて,実用化に向けた周辺技術開発を実施している。
図5|イジング計算機の技術レイヤ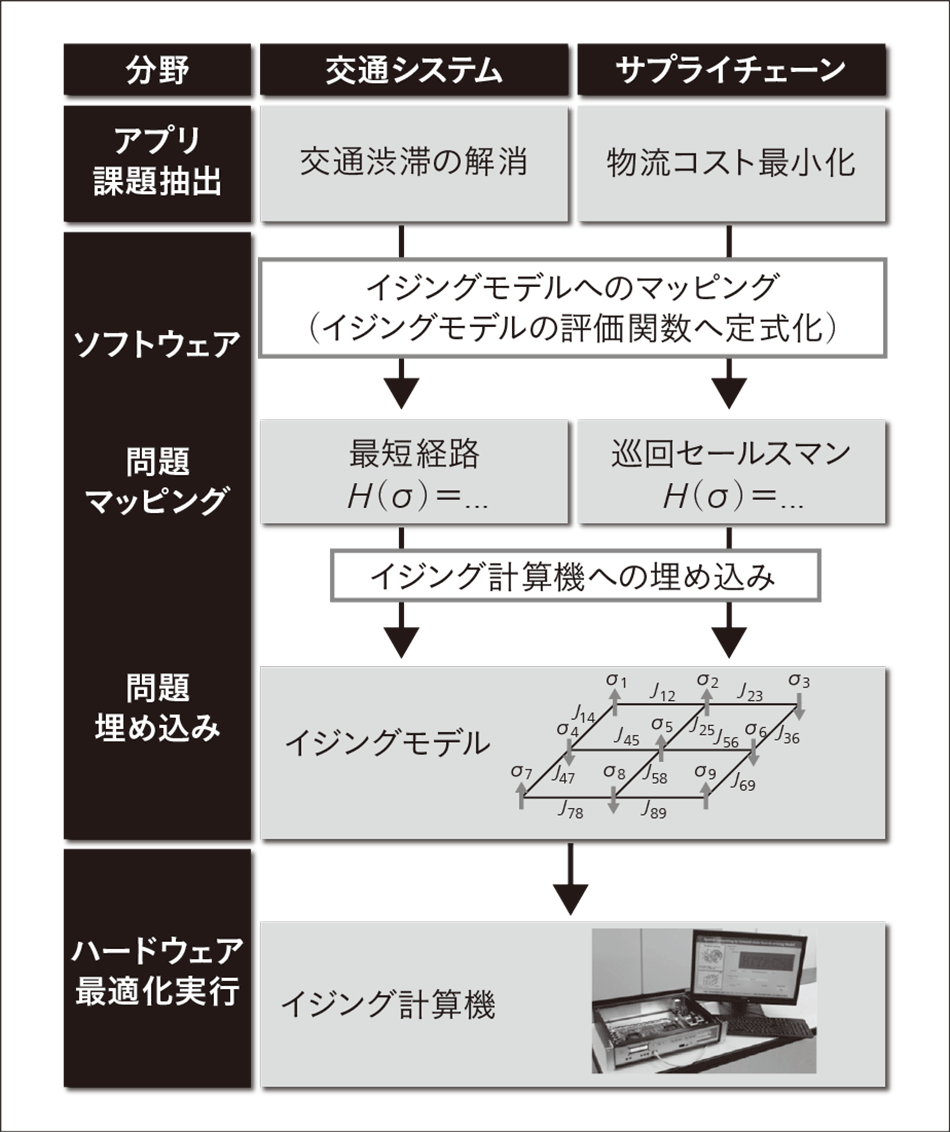 社会問題から課題を抽出するアプリレイヤ,抽出した課題を計算機に入力するために変換するソフトウェアレイヤ,実際に計算を実行するハードウェアレイヤでの技術開発が必要となる。
社会問題から課題を抽出するアプリレイヤ,抽出した課題を計算機に入力するために変換するソフトウェアレイヤ,実際に計算を実行するハードウェアレイヤでの技術開発が必要となる。
CMOSイジング計算機を実用化するには,計算機のハードウェアのみならず実際のアプリケーションの開発やそのアプリケーションをハードウェアに載せるためのソフトウェア技術が必要となる。本章では,CMOSイジング計算機の実用化に向けて必要な技術レイヤを説明し,その一つであるソフトウェア技術の一例を概説する。
実際の社会問題を解く際に必要なイジング計算機の技術レイヤを示す(図5参照)。実際の社会システムから解くべき課題を抽出するアプリケーションレイヤ,抽出した課題をイジング計算機のハードウェアに入力可能とするソフトウェアレイヤ,そして実際に計算を実行するハードウェアのレイヤが必要となる。
特にソフトウェアの技術は,抽出した最適化問題をイジングモデルのエネルギー関数の式に定式化するマッピング技術と,マッピングしたイジングモデルのトポロジを実際のイジング計算機のハードウェアが持っているトポロジに変換するグラフ埋め込み技術が必要となる。これらのソフトウェア技術の開発は,数学的な知識が求められるものであり,われわれは2016年に立ち上げた日立北大ラボにおいて北海道大学と連携して開発を進めている。また,前章で説明した第二世代のプロトタイプを効果的に用いることで,これらのソフトウェア技術の開発が可能となる。
実際の社会課題をマッピングしたイジングモデルは,スピン間で複雑なつながりを持っている。一方で,CMOSイジング計算機では,ハードウェアの制約からスピン間のつながりは単純な構成となる。例えば,CMOSイジング計算機が図6(a)に示す対角線付き格子グラフ(ハードウェアグラフ)Gを持つとする。第二世代プロトタイプでは,グラフGよりも複雑なつながりを持っている。グラフGの最大次数は8である一方,同図(b)に示すグラフHの最大次数は10である。ゆえにグラフHはグラフGのサブグラフではなく,グラフHを持つイジングモデルは直接CMOSイジング計算機では表現できない。
この問題を解決するため,1頂点を複数の頂点で置換する手法が提案されている5)。グラフHの頂点viを2個の頂点vi,1およびvi,2に分解し,同図(c)に示すグラフH'を作成する。この複製した頂点集合を頂点viの頂点集合φ(vi)と呼ぶ。φ(vi)に含まれる頂点間の相互作用を適切に定めると,グラフHを持つイジングモデルの基底状態におけるスピンの値は,グラフH'を持つイジングモデルの基底状態におけるスピンと一致する。また,グラフH'の最大次数は6で,グラフGのサブグラフである。このように頂点集合を形成することで,基底状態を変化させることなくグラフ変換が可能になり,イジングモデルをイジング計算機に埋め込むことができる。
イジング計算機では半導体回路で大規模なイジングモデルを表現するため,規則的な構造を持つイジングモデルの実装が前提となり,頂点分割を用いたグラフ変換が避けられない。この変換はスピン数を増加させるため,大規模な問題を解くためには頂点分割を可能な限り抑制しなければならない。つまり,同図(a)のように埋め込みが自明でないグラフが与えられたとき,頂点分割を抑制しつつ埋め込むアルゴリズムが必要となる。その手法の一つとして,CGME(Contractive Graph Minor-embedding)と呼ぶ技術を提案している6)。図7にグラフの規模と埋め込みにかかる時間の関係を示す。CGMEを使うことで,従来手法7)と比較して2桁以上高速にグラフを埋め込むことが可能となる。
社会イノベーションの実現に向けて,組合せ最適化問題を効率的に解くCMOSイジング計算機を開発した。
求めている解は完全な最適解ではないが,実際の社会システムの最適化には使えるレベルであり,今回の半導体を用いたアプローチは,使いやすさやスケーラビリティの観点から工学的に意味があると言える。CMOSイジング計算機の実用化に向けては,ハードウェア技術のみならず,それを利用するためのソフトウェア技術が必要となる。ソフトウェア開発を加速する第二世代のFPGAプロトタイプを試作するとともに,複雑な社会問題を規則的なイジング計算機のハードウェアに埋め込むソフトウェア技術を開発し,その実用化を推進している。