EXTRA CONTRIBUTIONA Method to Plan a Path to the SDGs from Sciences
Highlight
This article proposes a method for planning a path for approaching the Sustainable Development Goals starting from the sciences in the past possibly more quickly by means of an objective computer algorithm applied to data that is treated as representing an approximation of science as a whole. This study equates science as a whole with the corpus of all academic papers published to date, with it being represented in this case by a subset of these texts that is assumed to approximate its universal overall structure. As a first approximation, this article selects about 200 English-language journals that have been in publication for the last 50 years and are still being published regularly (meaning they have been sustained for 50 years or more), and takes approximately 5,000 papers from the latest issues of these journals (as of September 2019) to use as an example with which to demonstrate the proposed method. The path planned by this study is expressed in the form of a list of hypothetical papers. As a first approximation of this, this article obtains, for each science-goal pair, the 10 technical terms from different fields that, when added to the existing paper titles, result in the shortest distance to the corresponding Sustainable Development Goal. The specific procedure is as follows:
- The first step is to cluster the above collection of papers. A two-dimensional matrix is used in which the rows are the science clusters and the columns are the 17 Sustainable Development Goals. To make the matrix square, the number of science clusters is set to 17. The study assumes that all papers appearing in a particular issue of a journal belong to the same science cluster, and the sets of terms used in the English titles and journal names for all of the papers in the above latest journal issues are used as the “document” elements for clustering. In this article, the k-means clustering algorithm is used to cluster the document information, and the Latent Dirichlet Allocation (LDA) method is used to express a document element as a vector with a fixed dimension. The distance between two vectors is defined by cosine similarity. All of these are existing techniques. The dimensionality of the LDA vector space (number of topics) is determined by an optimization calculation that minimizes the variance of the number of elements in the clusters obtained by k-means clustering.
- The second step is to vectorize the 17 Sustainable Development Goals in the same way as was done for the 17 sciences above (that is, using the same methods of vectorization and the same definition of the distance between two vectors). The Sustainable Development Goals are defined as the sets of English terms that make up the text for each goal, with the text for the 169 targets and the 232 indicators being added to that for their corresponding goal. The distances between the vectors for the 17 Sustainable Development Goals and the vectors for the 17 science clusters (the gravity center of each cluster) are then calculated.
- The third step is path planning using the 17 × 17 distance matrix for the science clusters and Sustainable Development Goals as the objective function, the original document set as the initial point, and the Sustainable Development Goal text as the destination point. For the purposes of this article, the path is expressed by the set of new technological terms that, when added to the existing paper titles for the sciences, results in the shortest distance to the Sustainable Development Goals (as described above) for each of the 17 × 17 pairs of sciences and goals. To avoid the self-evident path in which the text of a Sustainable Development Goal itself is returned as a paper title, the terms to be added are selected from a set of approximately 4,000 candidates that appear two or more times in the original set of approximately 5,000 paper titles.
The relationships between each science cluster and goal were considered within the scope of the results of this experiment. As the entirety of academic documents encompasses tens of millions of papers, its approximation in this article by around 5,000 papers may not provide a meaningful volume of data, being at the level of an estimate based on a sample size of less than 1/10,000th of the total. However, because the study produced results in line with the subjective expectations of the author in terms of the experiment’s clustering results, the distance matrix for sciences and goals, and the obtained path from sciences to the Sustainable Development Goals, this demonstrates that the proposed method can have the potential to offer suggestions for the future application of science and indicates that further experimentation using a larger quantity of data is worth pursuing.
1. Introduction
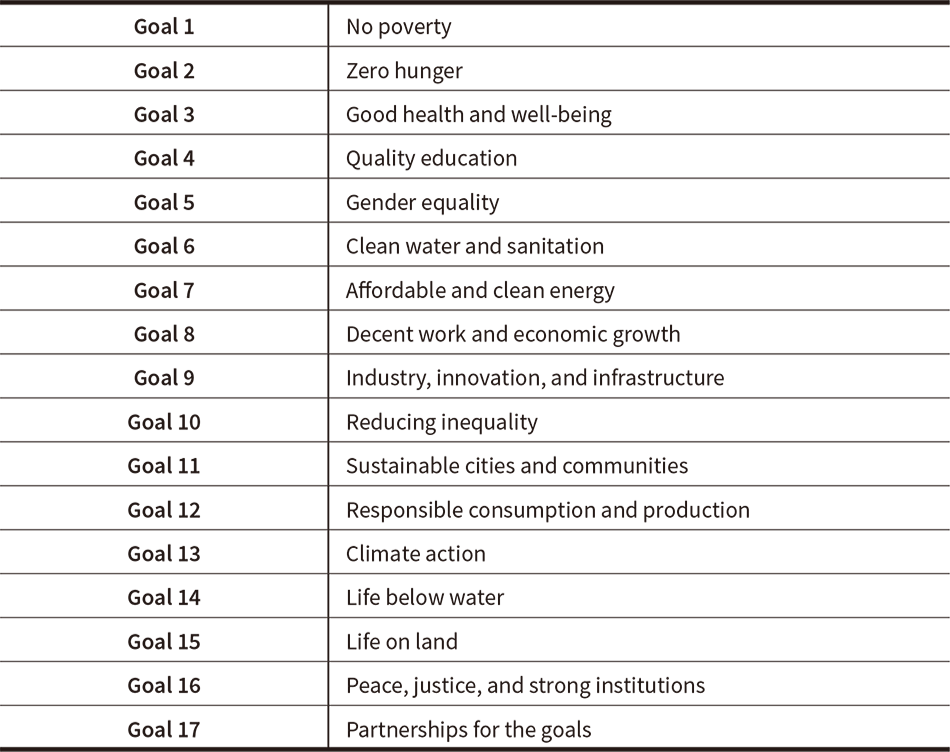
The Sustainable Development Goals (SDGs) are global goals for the sustainable development of humanity over the period from 2016 to 2030 and were set by the United Nations (UN) General Assembly in 2015. They are made up of 17 goals (as shown in Table 1), 169 targets, and 232 indicators(1). Because it is anticipated that science, technology, and innovation (STI) will play a major role in their achievement, activities are underway around the world under the banner of “STI for SDGs.” In Japan, the Engineering Academy of Japan (EAJ) has established an SDG project(2). The author has been appointed the leader of this project and has given presentations at venues that include an SDGs workshop at the annual meeting of the American Association for the Advancement of Science (AAAS) and a workshop at the STI Forum held at the UN headquarters in New York(3). A project for developing an STI roadmap for achieving the SDGs(4) was started later.
In recent years, meanwhile, work on the computer analysis of academic document data has advanced as a result of progress in information technology and artificial intelligence. One of the starting points for this work was a proposal for citation indexes published in 1955(5). A survey of research in this field has been published that includes this paper on citation indexes and extends up to the present day(6). Attempts have been made to take this work beyond the analysis of published papers by using the analysis results to make a strategy for future research. Examples include work on using the structural analysis of citation networks (the relationships between cited papers and the papers in which they are cited) to discover emerging fields of study(7). With regard to the SDGs specifically, work has also recently been published that analyzes the set of academic papers returned by a search using the keyword “sustainab*”(8).
In contrast to these prior works, the primary objective of this article is to determine whether there is a possibility of obtaining some form of guidance on how to achieve the SDGs through science from the analysis of academic document data by an objective computer algorithm. The second objective is to verify the natural language analysis capabilities of computers in recent years in the application of the macro analysis of science where human intuition seems to work. The third objective is to demonstrate a practical example of a new methodology for wide-angle research and development discussed in a separate article in this issue of Hitachi Review(3).
2. Reclassification of Science
This study equates science as a whole to the corpus of all academic papers published to date, with it being represented by a subset of these texts that is assumed to approximate its universal overall structure. The first step in determining, from a wide-angled view, paths to the SDGs for each science or scientific field is to perform clustering of this subset of academic papers.
One of the human classification methods for document is the Dewey Decimal System(9) published in 1876. This system provided the base for the Universal Decimal Classification(10) that was subsequently developed in 1905 and widely adopted by libraries around the world. In Japan, the Japanese Decimal Classification system(11) was developed in 1929 and is still in widespread use at libraries in Japan. All of these systems continue to undergo revision up to the present day. Meanwhile, a number of databases of technical papers and other such articles exist around the world, with the organizations that maintain them developing their own scientific categories with which to classify the articles they hold. A survey of the main technical document databases, their classification systems, and characteristics has also been published(12). This article, however, describes an attempt to use a computer algorithm to perform clustering for science in its entirety, covering papers from the past to the present day, based only on objective rules, explicitly avoiding the use of prior knowledge of the content of these existing classification systems.
The first step was to decide on a subset of academic papers that could be assumed to approximate the structure of the entire documents. As a first approximation to test the principle, this study selected about 200 English-language journals that have been in publication for the last 50 years and still are being published regularly (meaning they have lasted for 50 years or more), and took approximately 5,000 papers from the latest issues of these journals (as of September 2019) to use as an example with which to demonstrate the proposed method. Next, a clustering analysis was performed on this subset of academic papers. A two-dimensional matrix was used in which the rows are the science clusters and the columns are the 17 SDGs. To make the matrix square, the number of science clusters was set to 17. It is assumed that all papers appearing in the latest issue of a journal belong to the same science cluster, with the sets of terms used in the English titles of all of the papers in a particular issue of a journal being used as the document elements for clustering.
The first step is to vectorize each document element with fixed dimensions. Various methods have been proposed for transforming document text into vectors and, in recent years, have been widely used on actual problems. These include the Word2Vec model that uses a neural network to convert words into characteristic vectors by using the words that appear in the vicinity of words of interest(13), the Doc2Vec model that extends this to multiple documents(14), the Latent Dirichlet Allocation (LDA) method that is based on a model in which documents are generated probabilistically from a mixture of latent topics(15), and the term frequency–inverse document frequency (tf-idf) method that is based on the importance of each word that appears in a document(16). In this study, the LDA method was used to express each document element by a vector with fixed dimensions based on considerations that include prior knowledge and dependence on the given parameters. The dimensionality of the LDA vector space (number of topics) was treated as a variable and determined by an optimization for which the objective function was the variance in the number of elements in each cluster obtained by clustering (as described below). The dimensionality that minimized this variance was chosen. Prior to vectorization, the text is preprocessed by stemming (extraction of word stems from different verb tenses or the singular or plural forms of nouns and so on), and the exclusion of stop words (prepositions or other words that appear frequently in papers independent of content and would be likely to have little relationship to the vector that characterizes the text).
A general method that has been proposed for sample clustering in a multi-dimensional space is to use an iterative algorithm that first assigns each sample to an initial cluster and calculates the gravity center of each cluster. The samples are then assigned to new clusters based on which center they are closest to and the process is repeated(17). This is called the k-means method(18). Methods that work by assuming the probability distribution for the relationship between sample and cluster(19) have also come to be widely used, especially the Gaussian mixture model (GMM)(20) due to the improvements in computer performance over recent years. In this case, the above k-means method was used to specify the number of clusters. For the repeatability of experimentation, a fixed seed was used with random numbers to assign initial clusters. Also, cosine similarity (cosine of the angle between two vectors) was used to determine the distance between vectors in multi-dimensional space.
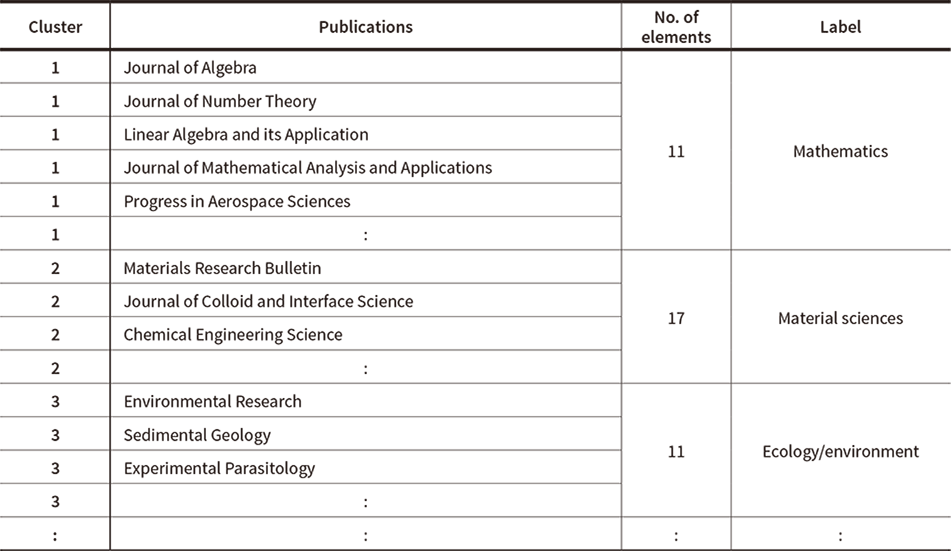
Table 2 shows some of the results of the experiment. The “Cluster” column contains the cluster numbers (1 to 17) obtained by applying the above clustering algorithm to the titles of the papers appearing in the latest edition of the academic journals in the “Publications” column. The “No. of elements” column contains the number of journals that belong to those clusters. The cluster numbers are identifiers only, with no meaning attached to their value or ordering. The “Label” column contains a name given to each cluster by the author for the purposes of convenience. As the 22 disciplines used as the top level of classification by the Essential Science Indicators (ESI)(12) are similar in number to the 17 clusters used here, these were used as a basis for naming.
Along with those classifications that were comparatively close to what the author would have anticipated, there were also some cluster and journal pairings that clearly looked out of place based on expectations and existing scientific classifications. It is expected that increasing the number of selected journals and papers has the potential to make the number of these low enough to ignore, at least for the purposes of the objective here, which is to suggest a path from each science cluster toward approaching the SDGs.
3. Distance between Science and SDGs
The next step was to determine the distances from each of the 17 science clusters obtained above to each of the SDGs. First, the document for each of the 17 SDGs was defined as the set of English terms that make up the text for each goal, with the text for the 169 targets being added to that for their corresponding goal. The vector for each of these was obtained using the same definition of distance, the same algorithm, and the same parameters as above. Next, the gravity center of the document vectors for each science cluster was calculated. The distances from the vectors for the text of each of the 17 SDGs to the gravity center of the science cluster document vectors were then calculated using cosine similarity, in the same way as above. The results formed a 17 × 17 matrix.
Table 3 shows the results of the distance calculation as described in the section above. The table shows the 17 × 17 matrix that contains the distances between the gravity center of the document vectors for sciences 1 to 17 (as defined above) and the vectors for the document for each SDG 1 to 17 (goal text and text for those of the 169 targets and 232 indicators that relate to the goal). These distances are defined in terms of cosine similarity (cosine of the angle between two vectors), with 1 being the minimum distance (closest) and 0 being the maximum (most distant). The table highlights in bold text those cells with the closest distance (maximum cosine similarity) for each of the SDGs. While the mappings of sciences to SDGs are not generally one-to-one, the experiment shows that eight of the 17 sciences make the greatest contributions to more than one of the 17 goals. The number rises to 13 when the sciences that make the three greatest contributions are counted. This could be described as providing a quantitative explanation of the idea that, rather than only specific scientific disciplines, most of the sciences can make a significant contribution to the SDGs.
In the experimental results, while science cluster 1 (labeled “Mathematics” in Table 2) has a comparatively close relationship with Goal 15 (Life on land), Goal 2 (Zero hunger), and Goal 6 (Clean water and sanitation), in each case an even closer cluster exists, such that the experiment does not show it as being closest to any of the goals. Conversely, the fact that it has the largest distance from Goal 4 (Quality education) represents an appropriate result given how far removed SDG text that talks about education for all people is from the text found in leading-edge research papers in mathematics. In the experiment described in the following section, however, the tendency for the distance to be shortened by adding particular technical terms to each paper in each science cluster is greater for mathematics than for other sciences. This can be interpreted as indicating that, the farther away a science is, the greater the potential for getting closer to the SDGs through combination with different scientific disciplines. The results also show that science cluster 2 (Material sciences) is closer than science cluster 1 (Mathematics) for 15 of the 17 SDGs. In particular, it is notably closer for Goal 6 (Clean water and sanitation), Goal 11 (Sustainable cities and communities), and Goal 10 (Reduced inequalities), among others. Science cluster 3 (Ecology/environment) has a close relationship with Goal 3 (Good health and well-being), Goal 16 (Peace, justice, and strong institutions), and Goal 17 (Partnership for the goals).
Table 3—Distance between Science and SDGs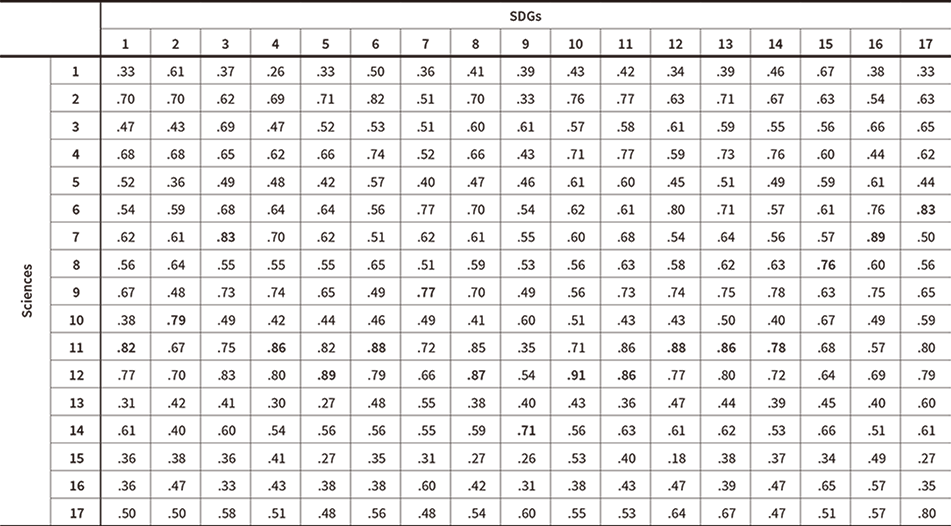 Distances are defined in terms of cosine similarity, with 1 being closest and 0 being most distant.
Distances are defined in terms of cosine similarity, with 1 being closest and 0 being most distant.
On the other hand, looking at science from the perspective of the SDGs, the results for Goal 7 (Affordable and clean energy) and Goal 9 (Industry, innovation, and infrastructure), for example, do not show that science and the SDGs are particularly close despite these being two areas where the author would expect science to have a comparatively high possibility of proving beneficial. In fields like this, as for the basic sciences discussed above, while this could be seen as indicating that this method works more effectively in terms of using path planning to reduce the distance to the SDGs, it cannot be ruled out that the number of journals and papers used in this article as the initial approximation data is below the threshold needed to provide a meaningful result.
4. Path from Science to the SDGs
Path planning was performed using the 17 × 17 distance matrix for the science clusters and SDGs obtained above as the objective function, the set of original documents as the initial point, and the SDG documents as the destination. Particulary in the field of robotics research, a variety of algorithms have been proposed for planning a path from an initial point to a destination under various conditions, such as the objective function and the constraints about obstacles. Most of these adopt a heuristic approach, especially when the number of dimensions is high(21). Optimal path planning methods have also been developed, especially for cases where the uncertainty in localizing the robot position is quantifiable(22) at the time of planning.
While the planned path of this study is expressed in the form of a list of hypothetical papers, for the purpose of this article, this is defined as the top 10 terms for each science-goal pair in the 17 × 17 matrix of sciences and SDGs that result in the shortest distance to the SDG when technical terms from different sciences are added to the existing paper titles for the science. In order to avoid self-evident solutions in which the text of an SDG itself is returned as a paper title, the candidate terms are chosen from the technical terms in the original set of scientific paper titles. For this experiment, this gave a set of approximately 4,000 candidate words, being those among the total of approximately 10,000 unique words left after the preprocessing described earlier in this article (stemming and exclusion of stop words) that appear two or more times in the titles. The search covered all the 4,000 of these words.
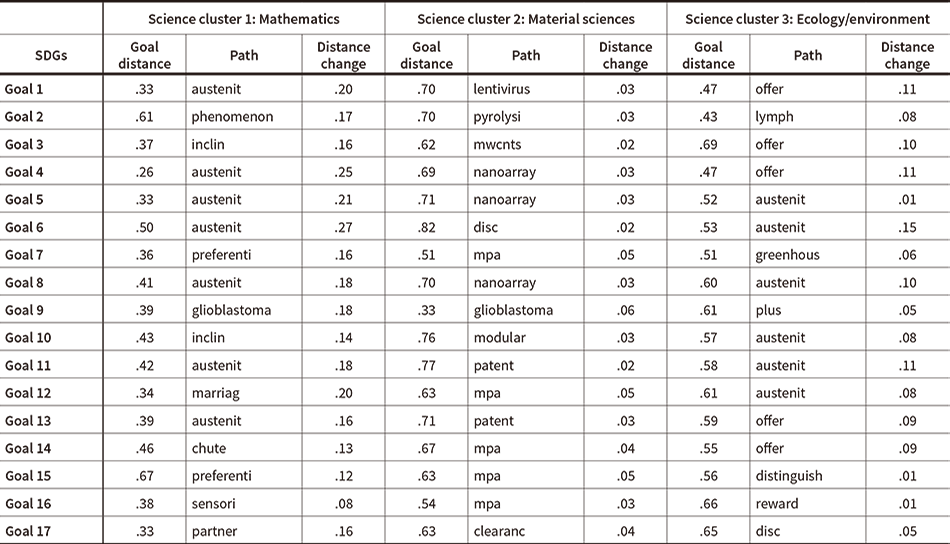
Table 4 shows a part of the experimental results. Sciences 1, 2, and 3 in the table are, respectively, those labeled mathematics, material sciences, and ecology/environment in Table 2. The “Goal distance” column lists the distances from the science in its current form to the SDG. The numbers in this column are taken directly from the corresponding row and column in Table 3. The “Path” column lists one of the top 10 technical terms from the titles of papers in different scientific fields that, when added to the paper titles for this science, shorten the goal distance by a large amount. In 42 of the 51 (3 × 17) cases, it is the top-ranked term that is listed. Three of the top-ranked terms that the author deemed difficult to explain were replaced by the second-ranked term. As described below, while there were numerous instances of the same term having the highest rank for multiple pairs, in three of these cases the second-ranked term was a distinctive one. In these cases also, the second-ranked term was listed instead. In three more cases, the second-ranked term was deemed by the author to better express the science/goal pair. These, too, were used. In all of the above cases, substitutions were only made when the difference between the distance-reduction effects of the first- and second-ranked terms was small enough. The “Distance change” column lists the difference between the new and old distances. That is, the new distance to the goal (after it has changed as a result of adding a term) minus the value of the “Goal distance” column. It is hypothesized that the larger this value is, the greater the potential contribution of research strategy to the SDGs will be.
While science cluster 1 (Mathematics) overall has a long distance from the SDGs, as noted above, the tendency is for this distance to be considerably shortened by the addition of particular technical terms from other disciplines. In the cases of Goal 6 (Clean water and sanitation), Goal 4 (Quality education), Goal 12 (Responsible consumption and production), and Goal 1 (No poverty), for example, the distance reduction exceeded 0.20, an amount not seen for any of the other science clusters in the study. While science cluster 2 (Material sciences) overall is a short distance to the SDGs, as noted above, the tendency is for the addition of single technical terms from other disciplines to result in very little reduction of this distance. However, the goals for which the percentage distance reduction is relatively high are Goal 9 (Industry, innovation, and infrastructure), Goal 7 (Affordable and clean energy), Goal 12 (Responsible consumption and production), and Goal 15 (Life on land), a result that is in line with the author’s expectations as to where materials science could contribute to the SDGs. The overall tendency for science cluster 3 (Ecology/environment) is for similar results to science cluster 2 (Material sciences). However, the goals with a high percentage distance reduction include Goal 14 (Life below water), Goal 6 (Clean water and sanitation), Goal 11 (Sustainable cities and communities), Goal 4 (Quality education), and Goal 1 (No poverty), indicating that the potential contribution is in completely different fields to those for material sciences indicated above, with this result being in line with the author’s expectations too.
The example terms listed in the “Path” column of the table include terms like “austenit” for mathematics and ecology/environment, “mpa” (megapascal) for material sciences, and “offer” for ecology/environment that are identified as beneficial for a large number of goals, with the same term, “glioblastoma” notably appearing for all three science clusters in the case of Goal 9 (Industry, innovation, and infrastructure). (Note that, for science cluster 3, “glioblastoma” was ranked second after “plus”). Meanwhile, there are also terms that are distinctive and for which a plausible explanation could be given, including adding “lentivirus” and “pyrolysi” to material sciences for Goal 1 (No poverty) and Goal 2 (Zero hunger); adding “mwcnts” (multi-walled carbon nanotubes) and “nanoarray” to material sciences for Goal 3 (Good health and well-being), Goal 4 (Quality education), and Goal 5 (Gender equality); adding “greenhous” to ecology/environment for Goal 7 (Affordable and clean energy); and adding “sensori” and “partner” to mathematics for Goal 16 (Peace, justice, and strong institutions) and Goal 17 (Partnership for the goals). While it cannot be ruled out that the number of journals and papers used in this article as the initial approximation data is below the threshold for the analysis of these, such that it potentially does not provide meaningful results, there is the possibility that experiments carried out using sufficient data could provide suggestions for various disciplines and future research plans.
5. Conclusions
This article has proposed a method for planning a path from sciences to the SDGs using an objective computer algorithm for clustering a set of documents that is assumed to approximate the entirety of past academic papers into 17 science clusters, then calculating the 17 × 17 matrix containing the distances from each of these 17 science clusters to each of the 17 SDGs, and then using this as the objective function to search for the path of papers that have the potential to address the SDGs more quickly in the future. An experiment was conducted using approximately 5,000 papers to verify the method. The author’s commentary on the results was presented.
As the entirety of academic documents encompasses tens of millions of papers, it may well be that the 5,000 or so papers used as an initial approximation in this article might not provide a meaningful volume of data, being at the level of an estimate based on a sample size of less than 1/10,000th of the total. However, because the study produced results in line with the subjective expectations of the author in terms of the experiment’s clustering results, the distance matrix for sciences and SDGs, and the obtained path from sciences to the SDGs, this results in the conclusion that the proposed method has the potential to offer suggestions when used in practice and indicates that further experiments using larger quantities of data are worth pursuing.
REFERENCES
- 1)
- “The 2030 Agenda for Sustainable Development,” United Nations, A/RES/70/1 (2015).
- 2)
- H. Takeda, “The SDGs Project of the Engineering Academy of Japan,” Trends in the Sciences, Vol. 23, No. 1, pp.60–63 (2018) in Japanese.
- 3)
- H. Takeda, “The SDGs and Social Innovation,” Hitachi Review, 69, pp.138–140 (Feb. 2020).
- 4)
- “A Guidebook for the Preparation of STI for SDGs Roadmap, Draft for Consultation,” The Fourth STI Forum, The United Nations, New York (2019).
- 5)
- E. Garfield, “Citation Indexes for Science: A New Dimension in Documentation through Association of Ideas,” Science, Vol. 122, pp.108–111 (1955).
- 6)
- S. Fortunato et al., “Science of Science,” Science, No. 359 (2018).
- 7)
- N. Shibata, “Detecting Emerging Research Fronts Based on Topological Measures in Citation Networks of Scientific Publications,” Technovation No. 28, pp.758–775 (2008).
- 8)
- K. Asatani et al., “Scientific Research on Sustainability: A Metaanalysis of Academic Papers about Sustainability and the Sustainable Development Goals,” The 14th Conference on Sustainable Development of Energy, Water, and Environment Systems, Croatia (2019).
- 9)
- M. Dewey, “Classification and Subject Index for Cataloguing and Arranging the Books and Pamphlets of a Library,” Project Gutenberg eBook (1876).
- 10)
- “Manuel du répertoire bibliographique universel,” Institut International de Bibliographie (1905).
- 11)
- K. Mori, “Japanese Decimal Classification: Classification and Indexing of Books in Japanese, Chinese, and Western Languages,” Mamiya Shoten (1929) in Japanese.
- 12)
- N. Onodera, “Subject Cataloging of Publications Databases,” The Journal of Information Science and Technology, Vol.66, No.6, pp.272–276 (2016) in Japanese.
- 13)
- T. Mikolov et al, “Distributed Representations of Words and Phrases and their Compositionality,” Neural Information Processing Systems Conference, Lake Tahoe, NV (2013).
- 14)
- L. Quoc et al., “Distributed Representations of Sentences and Documents,” Proceedings of the 31st International Conference on Machine Learning, Beijing, China (2014).
- 15)
- J. Pritchard et al., “Inference of Population Structure Using Multilocus Genotype Data,” Genetics, Vol. 155, No. 2, pp.945–959 (2000).
- 16)
- K. Jones, “A Statistical Interpretation of Term Specificity and its Application in Retrieval,” Journal of Documentation, Vol. 28, No. 1, pp.11–21 (1972).
- 17)
- H. Steinhaus, “Sur la division des corps matériels en parties,” Bulletin de l’Académie Polonaise des Sciences, Classe 3, pp.801–804 (1957).
- 18)
- J. MacQueen, “Some Methods for Classification and Analysis of Multivariate Observations,” Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, pp.281–297 (1967).
- 19)
- G. McLachlan et al., “Finite Mixture Models,” John Wiley & Sons, Inc. (2000).
- 20)
- C. Rasmussen, “The Infinite Gaussian Mixture Model,” Advances in Neural Information Processing Systems 12, MIT Press, MIT Press, pp.554–560 (2000).
- 21)
- J.-C. Latombe, “Robot Motion Planning,” Springer Science & Business Media (2012).
- 22)
- H. Takeda et al., “Planning the Motions of a Mobile Robot in a Sensory Uncertainty Field,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 16, No. 10, pp.1002–1017 (1994).